一 : 一个边长为0.1米的正方体,重100牛顿,放在面积为1米2的水平圆桌面的中央,求该正方体对桌面的压强( )
一个边长为0.1米的正方体,重100牛顿,放在面积为1米2的水平圆桌面的中央,求该正方体对桌面的压强( )
A.1×103Pa
B.1×104Pa
C.1×102Pa
D.1×105Pa
一个边长为0.1米的正方体,重100牛顿,放在面积为1米2的水平圆桌面的中央,求该正方体对桌面的压强( )的参考答案
正方体对桌面的压力:F=G=100N,
正方体面积S=0.1m×0.1m=0.01m2,
正方体对桌面的压强:P=
| F |
| S |
| 100N |
| 0.01m2 |
故选B.

二 : 一块正方形地砖的面积为0.25平方米,则其边长是______米.
| 一块正方形地砖的面积为0.25平方米,则其边长是______米. |
| 设边长为x, 则x2=0.25, 解得x=0.5或x=-0.5, ∵边长为正,负值舍去, ∴其边长是0.5米 故结果为:0.5米. |
考点:
考点名称:算术平方根概念:若一个正数x的平方等于a,即x2=a,则这个正数x为a的算术平方根。
规定:0的算术平方根是0。
表示:a的算术平方根记为
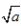 ,读作“根号a”。
,读作“根号a”。注:只有非负数有算术平方根,而且只有一个算术平方根。
平方根和算术平方根的区别与联系:
区别:
(1)定义不同:如果一个数的平方等于a,则这个数叫做a的平方根;非负数a的非负平方根叫做a的算术平方根。
(2)个数不同:一个正数有两个平方根,它们互为相反数;而一个正数的算术平方根只有一个。
(3)表示方法不同:正数a的平方根表示为±
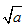 ,正数a的算术平方根表示为
,正数a的算术平方根表示为 。
。(4)取值范围不同:正数的算术平方根一定是正数;正数的平方根一正一负,两数互为相反数。
联系:
(1)具有包含关系:平方根包含算术平方根,算术平方根是平方根的一种,是正的平方根。
(2)存在条件相同:只有非负数才有平方根和算术平方根。
(3)0的平方根,算术平方根均为0。开平方:求一个数的平方根的运算,叫做开平方。
注:
(1)平方和开平方的关系是互为逆运算;
(2)乘方是求根的途径,开平方是一种运算,是求平方根的过程;
(3)开方的方式是根号形式。电脑根号的打法:
比较通用:
左手按住换档键(Alt键)不放,接着依次按41420然后松开左手,根号√ ̄就出来了。
运用Word的域命令在Word中根号:
首先按住Ctrl+F9,出现{}后,在{}内输入EQ空格r(开方次数,根号内的表达式),最后按住Shift+F9,就会生成你所要求的根式
1.平方根
一个正数的平方根有两个,它们互为相反数。比如 9 的平方根是3,-3。而5的平方根是√5,-√5。规定,零的平方根是0。负数没有平方根。
2.算术平方根是指一个正数的正的平方根。比如 9 的算术平方根是±3。而5的算术平方根是±√5。规定,零的算术平方根是0。
算术平方根是定义在平方根基础上,因此负数没有算术平方根。
3.实数a的算术平方根记作√ ̄a,其中a≥0,根据以上定义有√ ̄a≥0。
三 : 如图,已知图形中的圆的半径为6厘米,右下部是一个正方形,求阴影部分的面积和周长.
如图,已知图形中的圆的半径为6厘米,右下部是一个正方形,求阴影部分的面积和周长.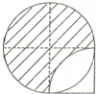 |
阴影部分的面积为:
=27×3.14+(36-28.26), =84.78+7.74, =92.52(平方厘米); 阴影部分的周长为:3.14×6×2=37.68(厘米), 答:阴影部分的面积是92.52平方厘米,周长为37.68厘米. |
考点:
考点名称:圆的周长圆的周长计算公式:圆的周长=直径×圆周率=2×半径×圆周率;C=πd=2πr。(r—半径,d—直径,π—圆周率)
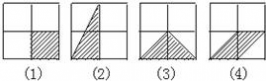
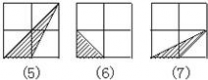
四 : 已知图中A,B分别表示正方形网格上的两个轴对称图形(阴影部分),其面积分别记为S1,S2(网格中最小
| 已知图中A,B分别表示正方形网格上的两个轴对称图形(阴影部分),其面积分别记为S1,S2(网格中最小的正方形的面积为一个单位面积),请你观察并回答问题. (1)求s1和s2的值; (2)请你在图C中的网格上画一个面积为8个平方单位的轴对称图形.  |

 中,P为边
中,P为边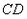 的中点,直线
的中点,直线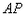 交圆于点
交圆于点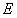 .
.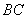 上一动点,当
上一动点,当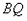 长为何值时,三角形
长为何值时,三角形 与以
与以 为顶点的三角形相似.
为顶点的三角形相似. 
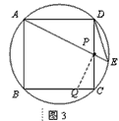
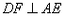 于点F.
于点F. 中,
中,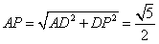
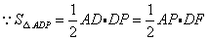

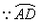 的度数为
的度数为

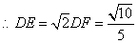
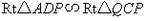 时有
时有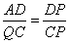
 .即Q点与B点重合,
.即Q点与B点重合,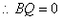
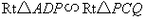 时,有
时,有
 ,即
,即 
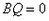 或
或 时,三角形
时,三角形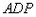 与以点
与以点 为顶点的三角形相似.
为顶点的三角形相似.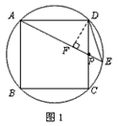

 。
。