一 : 如图,三棱柱ABCA1B1C1中,CA=CB,AB=AA1,∠BAA1=60°.(1)证明:AB⊥A
如图,三棱柱ABC A1B1C1中,CA=CB,AB=AA1,∠BAA1=60°. A1B1C1中,CA=CB,AB=AA1,∠BAA1=60°.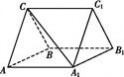 (1)证明:AB⊥A1C; (2)若AB=CB=2,A1C= 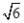 ,求三棱柱ABC ,求三棱柱ABC A1B1C1的体积. A1B1C1的体积. |
| (1)见解析 (2)3 |
(1)证明:取AB的中点O,连接OC,OA1,A1B. 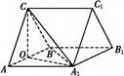 因为CA=CB,所以OC⊥AB. 由于AB=AA1,∠BAA1=60°, 故△AA1B为等边三角形, 所以OA1⊥AB. 因为OC∩OA1=O, 所以AB⊥平面OA1C. 又A1C?平面OA1C,故AB⊥A1C. (2)解:由题设知△ABC与△AA1B都是边长为2的等边三角形,所以OC=OA1= 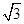 . .又A1C= 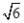 ,则A1C2=OC2+O ,则A1C2=OC2+O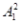 ,故OA1⊥OC. ,故OA1⊥OC.因为OC∩AB=O,所以OA1⊥平面ABC,OA1为三棱柱ABC  A1B1C1的高. A1B1C1的高.又△ABC的面积S△ABC= 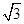 ,故三棱柱ABC ,故三棱柱ABC A1B1C1的体积V=S△ABC×OA1=3. A1B1C1的体积V=S△ABC×OA1=3. |
考点:
考点名称:柱体、椎体、台体的表面积与体积侧面积和全面积的定义:
(1)侧面积的定义:把柱、锥、台的侧面沿着它们的一条侧棱或母线剪开,所得到的展开图的面积,就是空间几何体的侧面积.
(2)全面积的定义:空间几何体的侧面积与底面积的和叫做空间几何体的全面积,
柱体、锥体、台体的表面积公式(c为底面周长,h为高,h′为斜高,l为母线)

柱体、锥体、台体的体积公式:

多面体的侧面积与体积:
| 多面体 | 图像 | 侧面积 | 体积 |
| 棱柱 |  | 直棱柱的侧面展开图是矩形 |  |
| 棱锥 |  | 正棱柱的侧面展开图是一些全等的等腰三角形, |  |
| 棱台 |  | 正棱台的侧面展开图是一些全等的等腰梯形,  |  |
旋转体的侧面积和体积:
| 旋转体 | 图形 | 侧面积与全面积 | 体积 |
| 圆柱 |  | 圆柱的侧面展开图的矩形: |  |
| 圆锥 |  | 圆锥的侧面展开图是扇形: |  |
| 圆台 |  | 圆台的侧面展开图是扇环: |  |
| 球 |  |  |  |
球的体积公式:
V球= ;
;
球的表面积:
S球面=
求球的表面积和体积的关键:
由球的表面积和体积公式可知,求球的表面积和体积的关键是求出半径。
常用结论:
1.若球的表面积变为原来的2倍,则半径变为原来的 倍.
倍.
2.若球半径变为原来的2倍,则表面积变为原来的4倍.
3.若两球表面积之比为1:2,则其体积之比是 .
.
4.若两球体积之比是1:2,则其表面积之比是 .
.
定义:
组合体的表面积与体积主要通过计算组成几何体的简单几何体的表面积与体积来求解。
组合体的表面积和体积与球有关的组合体问题:
一种是内切,一种是外接.解题时要认真分析图形,明确切点和接点的位置,确定有关元素间的数量关系,并作出合适的截面图.如球内切于正方体,切点为正方体各个面的中心,正方体的棱长等于球的直径;球外接于正方体,正方体的顶点均在球面上,正方体的体对角线长等于球的直径.球与旋转体的组合,通常作它们的轴截面解题,球与多面体的组合,通过多面体的一条侧棱和球心,或”、点。
求几何体的体积的几种常用方法:
(1)分割求和法:把不规则的图形分割成规则的图形,然后进行体积求和;
(2)补形法:把不规则形体补成规则形体,不熟悉形体补成熟悉形体,便于计算其体积;
常见的补形方法:
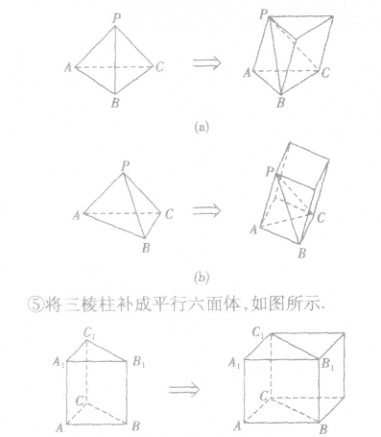
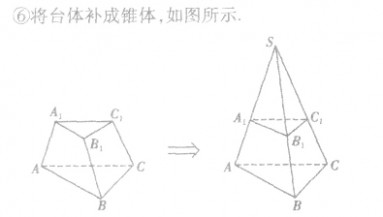
(3)等体积转化法:从不同的角度看待原几何体,通过改变顶点和底面,利用体积不变的原理,求原几何体的体积。
二 : 三棱柱

很简单
主要材料
:| 彩纸适量 |
所需工具
:| 爪爪一双 |
制作步骤
:第1步:

此乃是彩纸。。
(www.61k.com)第2步:

对折。
第3步:

打开。
第4步:

沿着刚才折的线,,对折。
第5步:

再打开。。。
第6步:

四个角折上。
第7步:

再对折。
第8步:

再再打开,再再对折。
第9步:

第10步:

两端插上,然后三棱柱就完成了。
小贴士
:叠多几个,,比如六个,可以做个笔筒,如果有不会的,,可以私我哦。
三 : 小三棱柱手工制作
看图
主要材料
:| 纸带 |
所需工具
:| 剪刀 |
制作步骤
:第1步:

第2步:

第3步:

第4步:

两边重叠
第5步:

第6步:

第7步:

第8步:

一直反复折,直到折完
第9步:

第10步:

第11步:

折完后再展开
第12步:

顺着折印围成三棱柱型,然后一直顺势围下去
第13步:

第14步:

收尾时要剩下一小部分
第15步:

第16步:

第17步:

第18步:
